Publications

2025

1. Preprint

   Query Efficient Structured Matrix Learning

   Noah Amsel, Pratyush Avi, Tyler Chen, Feyza Duman Keles, Chinmay Hegde, Cameron Musco, Christopher Musco, and David Persson

   Jul 2025

   Abstract arXiv

   We study the problem of learning a structured approximation (low-rank, sparse, banded, etc.) to an unknown matrix $\mathbf{A}$ given access to matrix-vector product (matvec) queries of the form $\mathbf{x} \rightarrow \mathbf{A}\mathbf{x}$ and $\mathbf{x} \rightarrow \mathbf{A}^\top \mathbf{x}$. This problem is of central importance to algorithms across scientific computing and machine learning, with applications to fast multiplication and inversion for structured matrices, building preconditioners for first-order optimization, and as a model for differential operator learning. Prior work focuses on obtaining query complexity upper and lower bounds for learning specific structured matrix families that commonly arise in applications.

   We initiate the study of the problem in greater generality, aiming to understand the query complexity of learning approximations from general matrix families. Our main result focuses on finding a near-optimal approximation to $\mathbf{A}$ from any finite-sized family of matrices, $\mathcal{F}$. Standard results from matrix sketching show that $O(\log|\mathcal{F}|)$ matvec queries suffice in this setting. This bound can also be achieved, and is optimal, for vector-matrix-vector queries of the form $\mathbf{x},\mathbf{y}\rightarrow \mathbf{x}^\top\mathbf{A}\mathbf{y}$, which have been widely studied in work on rank-$1$ matrix sensing. Surprisingly, we show that, in the matvec model, it is possible to obtain a nearly quadratic improvement in complexity, to $\tilde{O}(\sqrt{\log|\mathcal{F}|})$. Further, we prove that this bound is tight up to log-log factors. Via covering number arguments, our result extends to well-studied infinite families. As an example, we establish that a near-optimal approximation from any linear matrix family of dimension $q$ can be learned with $\tilde{O}(\sqrt{q})$ matvec queries, improving on an $O(q)$ bound achievable via sketching techniques and vector-matrix-vector queries.

2. Preprint

   

   The Polar Express: Optimal Matrix Sign Methods and Their Application to the Muon Algorithm

   Noah Amsel, David Persson, Christopher Musco, and Robert M. Gower

   May 2025

   Blogs about our work by Ethan Epperly and Jianlin Su.

   Abstract arXiv Code

   Computing the polar decomposition and the related matrix sign function has been a well-studied problem in numerical analysis for decades. Recently, it has emerged as an important subroutine within the Muon algorithm for training deep neural networks. However, the requirements of this application differ sharply from classical settings: deep learning demands GPU-friendly algorithms that prioritize high throughput over high precision. We introduce Polar Express, a new method for computing the polar decomposition. Like Newton-Schulz and other classical polynomial methods, our approach uses only matrix-matrix multiplications, making it very efficient on GPUs. Inspired by earlier work of Chen & Chow and Nakatsukasa & Freund, Polar Express adapts the update rule at each iteration by solving a minimax optimization problem. We prove that this strategy minimizes error in a worst-case sense, allowing Polar Express to converge as rapidly as possible both in the early iterations and asymptotically. We also address finite-precision issues, making it practical to use in bfloat16. When integrated into the Muon training framework, our method leads to consistent improvements in validation loss when training a GPT-2 model on one billion tokens from the FineWeb dataset, outperforming recent alternatives across a range of learning rates.

3. Preprint

   

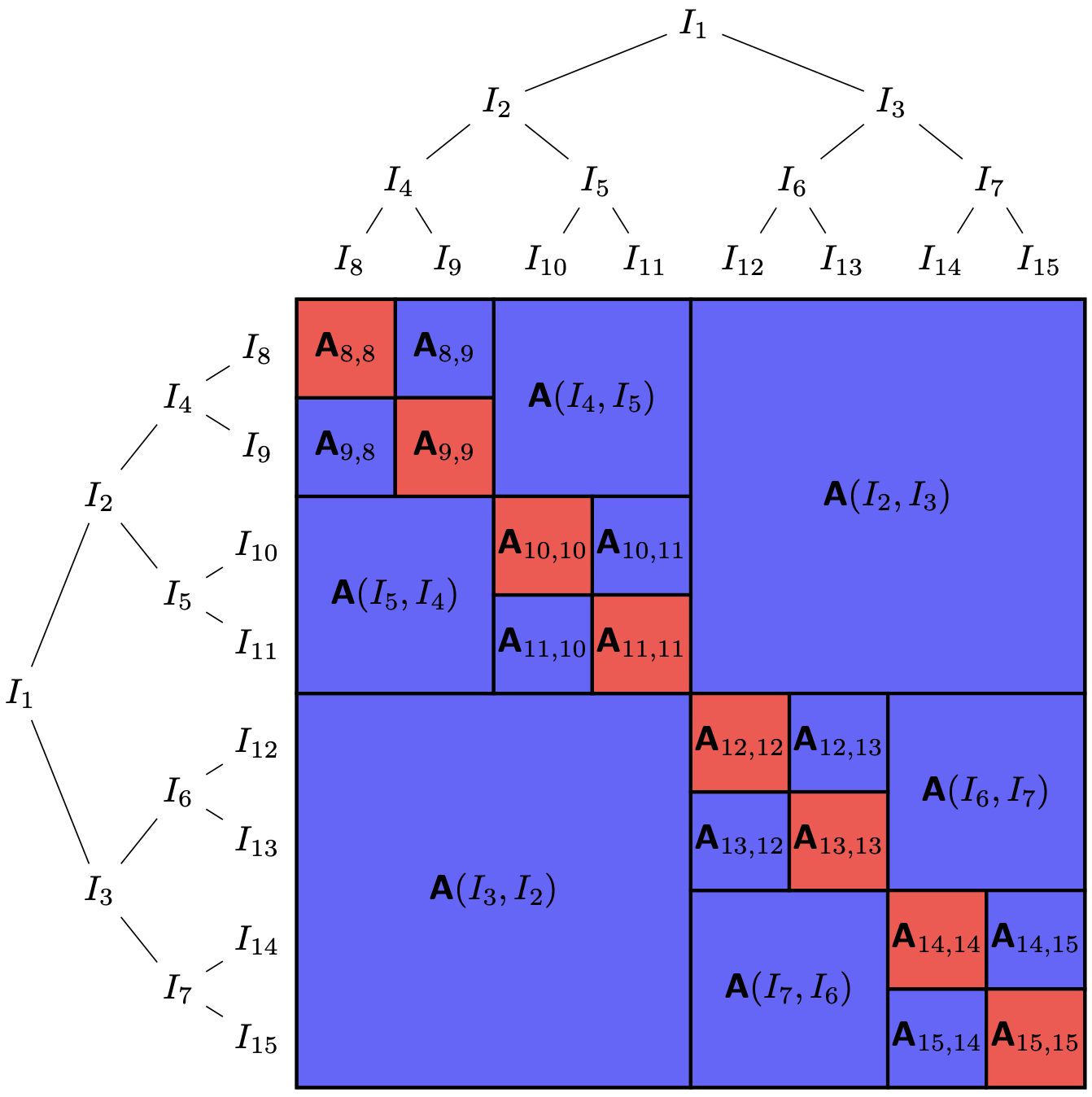   Quasi-optimal hierarchically semi-separable matrix approximation

   Noah Amsel, Tyler Chen, Feyza Duman Keles, Diana Halikias, Cameron Musco, Christopher Musco, and David Persson

   May 2025

   Abstract arXiv Code

   We present a randomized algorithm for producing a quasi-optimal hierarchically semi-separable (HSS) approximation to an $N \times N$ matrix $\mathbf A$ using only matrix-vector products with $\mathbf A$ and $\mathbf A^\top$. We prove that, using $O(k \log(N/k))$ matrix-vector products and $O(Nk^2 \log(N/k))$ additional runtime, the algorithm returns an HSS matrix $\mathbf B$ with rank-$k$ blocks whose expected Frobenius norm error $\mathbb E[\|\mathbf A - \mathbf B\|^2_F]$ is at most $O(\log(N/k))$ times worse than the best possible approximation error by an HSS rank-$k$ matrix. In fact, the algorithm we analyze in a simple modification of an empirically effective method proposed by Levitt & Martinsson [SISC 2024]. As a stepping stone towards our main result, we prove two results that are of independent interest: a similar guarantee for a variant of the algorithm which accesses A's entries directly, and explicit error bounds for near-optimal subspace approximation using projection-cost-preserving sketches. To the best of our knowledge, our analysis constitutes the first polynomial-time quasi-optimality result for HSS matrix approximation, both in the explicit access model and the matrix-vector product query model.

4. Preprint

   

   Compositional Reasoning with Transformers, RNNs, and Chain of Thought

   Gilad Yehudai, Noah Amsel, and Joan Bruna

   Mar 2025

   Abstract arXiv

   We study and compare the expressive power of transformers, RNNs, and transformers with chain of thought tokens on a simple and natural class of problems we term Compositional Reasoning Questions (CRQ). This family captures problems like evaluating Boolean formulas and multi-step word problems. Assuming standard hardness assumptions from circuit complexity and communication complexity, we prove that none of these three architectures is capable of solving CRQs unless some hyperparameter (depth, embedding dimension, and number of chain of thought tokens, respectively) grows with the size of the input $n$. We also provide a construction for each architecture that solves CRQs. For transformers, our construction uses depth that is logarithmic in the problem size. For RNNs, logarithmic embedding dimension is necessary and sufficient, so long as the inputs are provided in a certain order. (Otherwise, a linear dimension is necessary). For transformers with chain of thought, our construction uses $n$ CoT tokens. These results show that, while CRQs are inherently hard, there are several different ways for language models to overcome this hardness. Even for a single class of problems, each architecture has strengths and weaknesses, and none is strictly better than the others.

5. ICML

   Customizing the Inductive Biases of Softmax Attention using Structured Matrices

   Yilun Kuang, Noah Amsel, Sanae Lotfi, Shikai Qiu, Andres Potapczynski, and Andrew Gordon Wilson

   In Proceedings of the 42nd International Conference on Machine Learning (ICML), Jul 2025

   Abstract Journal Blog Poster Slides

   The core component of attention is the scoring function, which transforms the inputs into low-dimensional queries and keys and takes the dot product of each pair. While the low-dimensional projection improves efficiency, it causes information loss for certain tasks that have intrinsically high-dimensional inputs. Additionally, attention uses the same scoring function for all input pairs, without imposing a locality bias for neighboring tokens in the sequence. In this work, we address these shortcomings by proposing new scoring functions based on computationally efficient structured matrices with high ranks, including Block Tensor-Train (BTT) and Multi-Level Low Rank (MLR) matrices. On in-context regression tasks with high-dimensional inputs, our proposed scoring functions outperform standard attention for any fixed compute budget. On language modeling, a task that exhibits locality, our MLR-based attention method achieves improved scaling laws compared to both standard attention and variants of sliding window attention. Additionally, we show that both BTT and MLR fall under a broader family of efficient structured matrices capable of encoding either full-rank or locality biases, thereby addressing significant shortcomings of standard attention.

6. ICLR

   

   Quality over Quantity in Attention Layers: When Adding More Heads Hurts

   Noah Amsel, Gilad Yehudai, and Joan Bruna

   In International Conference on Representation Learning (ICLR), Apr 2025

   Abstract Journal Code Poster Slides

   Attention-based mechanisms are widely used in machine learning, most prominently in transformers. However, hyperparameters such as the number of attention heads and the attention rank (i.e., the query/key dimension) are set nearly the same way in all realizations of this architecture, without theoretical justification. In this paper, we prove that the rank can have a dramatic effect on the representational capacity of attention. This effect persists even when the number of heads and the parameter count are very large. Specifically, we present a simple and natural target function based on nearest neighbor search that can be represented using a single full-rank attention head for any sequence length, but that cannot be approximated by a low-rank attention layer even on short sequences unless the number of heads is exponential in the embedding dimension. Thus, for this target function, rank is what determines an attention layer's power. We show that, for short sequences, using multiple layers allows the target to be approximated by low-rank attention; for long sequences, we conjecture that full-rank attention is necessary regardless of depth. Finally, we present experiments with standard multilayer transformers that validate our theoretical findings. They demonstrate that, because of how standard transformer implementations set the rank, increasing the number of attention heads can severely decrease accuracy on certain tasks.

2024

1. Preprint

   Fixed-sparsity matrix approximation from matrix-vector products

   Noah Amsel, Tyler Chen, Feyza Duman Keles, Diana Halikias, Cameron Musco, and Christopher Musco

   Feb 2024

   Abstract arXiv Blog Code Slides

   We study the problem of approximating a matrix $\mathbf A$ with a matrix that has a fixed sparsity pattern (e.g., diagonal, banded, etc.), when $\mathbf A$ is accessed only by matrix-vector products. We describe a simple randomized algorithm that returns an approximation with the given sparsity pattern with Frobenius-norm error at most $(1+\epsilon)$ times the best possible error. When each row of the desired sparsity pattern has at most $s$ nonzero entries, this algorithm requires $O(s/\epsilon)$ non-adaptive matrix-vector products with $\mathbf A$. We also prove a matching lower-bound, showing that, for any sparsity pattern with $\Theta(s)$ nonzeros per row and column, any algorithm achieving $(1+\epsilon)$ approximation requires $\Omega(s/\epsilon)$ matrix-vector products in the worst case. We thus resolve the matrix-vector product query complexity of the problem up to constant factors, even for the well-studied case of diagonal approximation, for which no previous lower bounds were known.

2. NeurIPS

   

   Nearly Optimal Approximation of Matrix Functions by the Lanczos Method

   Noah Amsel, Tyler Chen, Anne Greenbaum, Cameron Musco, and Christopher Musco

   In The Thirty-eighth Annual Conference on Neural Information Processing Systems (NeurIPS), Dec 2024

   Also check out this follow up work.

   Spotlight! Abstract Journal Code Poster Slides

   Top 2% of NeurIPS submissions.

   Approximating the action of a matrix function $f(A)$ on a vector $\vec{b}$ is an increasingly important primitive in machine learning, data science, and statistics, with applications such as sampling high dimensional Gaussians, Gaussian process regression and Bayesian inference, principal component analysis, and approximating Hessian spectral densities. Over the past decade, a number of algorithms enjoying strong theoretical guarantees have been proposed for this task. Many of the most successful belong to a family of algorithms called Krylov subspace methods. Remarkably, a classic Krylov subspace method called the Lanczos method for matrix functions (Lanczos-FA) frequently outperforms newer methods in practice. Our main result is a theoretical justification for this finding: we show that, for a natural class of rational functions, Lanczos-FA matches the error of the best possible Krylov subspace method up to a multiplicative approximation factor. The approximation factor depends on the degree of $f(x)$'s denominator and the condition number of $A$, but not on the number of iterations $k$. Our result provides a strong justification for the excellent performance of Lanczos-FA, especially on functions that are well approximated by rationals, such as the matrix square root.

2023

1. Inf Inference

   

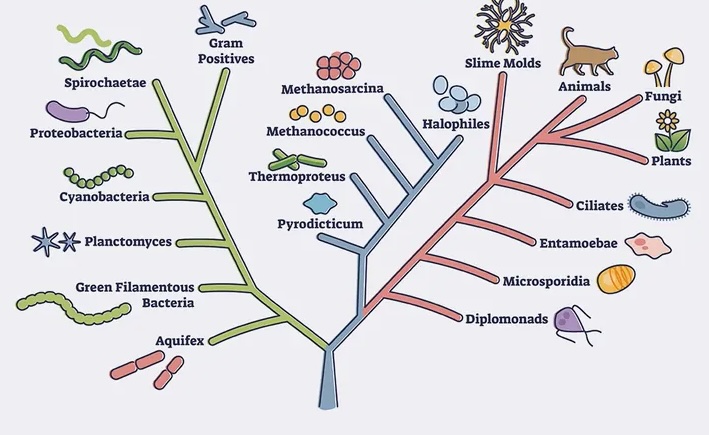   Spectral top-down recovery of latent tree models

   Yariv Aizenbud, Ariel Jaffe, Meng Wang, Amber Hu, Noah Amsel, Boaz Nadler, Joseph T Chang, and Yuval Kluger

   Information and Inference: A Journal of the IMA, Aug 2023

   Abstract Journal PDF Code Slides

   Modeling the distribution of high-dimensional data by a latent tree graphical model is a prevalent approach in multiple scientific domains. A common task is to infer the underlying tree structure, given only observations of its terminal nodes. Many algorithms for tree recovery are computationally intensive, which limits their applicability to trees of moderate size. For large trees, a common approach, termed divide-and-conquer, is to recover the tree structure in two steps. First, separately recover the structure of multiple, possibly random subsets of the terminal nodes. Second, merge the resulting subtrees to form a full tree. Here, we develop spectral top-down recovery (STDR), a deterministic divide-and-conquer approach to infer large latent tree models. Unlike previous methods, STDR partitions the terminal nodes in a non random way, based on the Fiedler vector of a suitable Laplacian matrix related to the observed nodes. We prove that under certain conditions, this partitioning is consistent with the tree structure. This, in turn, leads to a significantly simpler merging procedure of the small subtrees. We prove that STDR is statistically consistent and bound the number of samples required to accurately recover the tree with high probability. Using simulated data from several common tree models in phylogenetics, we demonstrate that STDR has a significant advantage in terms of runtime, with improved or similar accuracy.

2021

1. SIGCOMM

   

   Designing Data Center Networks Using Bottleneck Structures

   Jordi Ros-Giralt, Noah Amsel, Sruthi Yellamraju, James Ezick, Richard Lethin, Yuang Jiang, Aosong Feng, Leandros Tassiulas, Zhenguo Wu, Min Yee Teh, and Keren Bergman

   In Proceedings of the ACM SIGCOMM 2021 Conference, Aug 2021

   Abstract Journal Video Code

   This paper provides a mathematical model of data center performance based on the recently introduced Quantitative Theory of Bottleneck Structures (QTBS). Using the model, we prove that if the traffic pattern is textit{interference-free}, there exists a unique optimal design that both minimizes maximum flow completion time and yields maximal system-wide throughput. We show that interference-free patterns correspond to the important set of patterns that display data locality properties and use these theoretical insights to study three widely used interconnects---fat-trees, folded-Clos and dragonfly topologies. We derive equations that describe the optimal design for each interconnect as a function of the traffic pattern. Our model predicts, for example, that a 3-level folded-Clos interconnect with radix 24 that routes 10\% of the traffic through the spine links can reduce the number of switches and cabling at the core layer by 25\% without any performance penalty. We present experiments using production TCP/IP code to empirically validate the results and provide tables for network designers to identify optimal designs as a function of the size of the interconnect and traffic pattern.

2. SIMODS

   

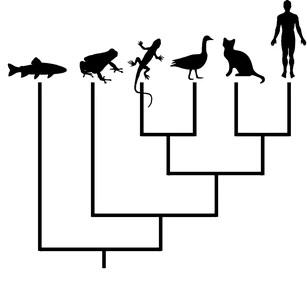   Spectral Neighbor Joining for Reconstruction of Latent Tree Models

   Ariel Jaffe, Noah Amsel, Yariv Aizenbud, Boaz Nadler, Joseph T. Chang, and Yuval Kluger

   SIAM Journal on Mathematics of Data Science (SIMODS), Aug 2021

   Abstract Journal PDF Code Slides

   A common assumption in multiple scientific applications is that the distribution of observed data can be modeled by a latent tree graphical model. An important example is phylogenetics, where the tree models the evolutionary lineages of a set of observed organisms. Given a set of independent realizations of the random variables at the leaves of the tree, a key challenge is to infer the underlying tree topology. In this work we develop spectral neighbor joining (SNJ), a novel method to recover the structure of latent tree graphical models. Given a matrix that contains a measure of similarity between all pairs of observed variables, SNJ computes a spectral measure of cohesion between groups of observed variables. We prove that SNJ is consistent and derive a sufficient condition for correct tree recovery from an estimated similarity matrix. Combining this condition with a concentration of measure result on the similarity matrix, we bound the number of samples required to recover the tree with high probability. We illustrate via extensive simulations that in comparison to several other reconstruction methods, SNJ requires fewer samples to accurately recover trees with a large number of leaves or long edges.

2020

1. INDIS

   Computing Bottleneck Structures at Scale for High-Precision Network Performance Analysis

   Noah Amsel, Jordi Ros-Giralt, Sruthi Yellamraju, James Ezick, Brendan Hofe, Alison Ryan, and Richard Lethin

   In 2020 IEEE/ACM Innovating the Network for Data-Intensive Science (INDIS), Nov 2020

   Abstract Journal PDF Slides

   The Theory of Bottleneck Structures is a recently-developed framework for studying the performance of data networks. It describes how local perturbations in one part of the network propagate and interact with others. This framework is a powerful analytical tool that allows network operators to make accurate predictions about network behavior and thereby optimize performance. Previous work implemented a software package for bottleneck structure analysis, but applied it only to toy examples. In this work, we introduce the first software package capable of scaling bottleneck structure analysis to production-size networks. Here, we benchmark our system using logs from ESnet, the Department of Energy's high-performance data network that connects research institutions in the U.S. Using the previously published tool as a baseline, we demonstrate that our system achieves vastly improved performance, constructing the bottleneck structure graphs in 0.21 s and calculating link derivatives in 0.09 s on average. We also study the asymptotic complexity of our core algorithms, demonstrating good scaling properties and strong agreement with theoretical bounds. These results indicate that our new software package can maintain its fast performance when applied to even larger networks. They also show that our software is efficient enough to analyze rapidly changing networks in real time. Overall, we demonstrate the feasibility of applying bottleneck structure analysis to solve practical problems in large, real-world data networks.

2019

1. BlackboxNLP

   Finding Hierarchical Structure in Neural Stacks Using Unsupervised Parsing

   William Merrill, Lenny Khazan, Noah Amsel, Yiding Hao, Simon Mendelsohn, and Robert Frank

   In Proceedings of the 2019 ACL Workshop BlackboxNLP: Analyzing and Interpreting Neural Networks for NLP, Aug 2019

   Abstract Journal PDF Code

   Neural network architectures have been augmented with differentiable stacks in order to introduce a bias toward learning hierarchy-sensitive regularities. It has, however, proven difficult to assess the degree to which such a bias is effective, as the operation of the differentiable stack is not always interpretable. In this paper, we attempt to detect the presence of latent representations of hierarchical structure through an exploration of the unsupervised learning of constituency structure. Using a technique due to Shen et al. (2018a, b), we extract syntactic trees from the pushing behavior of stack RNNs trained on language modeling and classification objectives. We find that our models produce parses that reflect natural language syntactic constituencies, demonstrating that stack RNNs do indeed infer linguistically relevant hierarchical structure.

2018

1. BlackboxNLP

   Context-Free Transductions with Neural Stacks

   Yiding Hao, William Merrill, Dana Angluin, Robert Frank, Noah Amsel, Andrew Benz, and Simon Mendelsohn

   In Proceedings of the 2018 EMNLP Workshop BlackboxNLP: Analyzing and Interpreting Neural Networks for NLP, Nov 2018

   Abstract Journal PDF Code

   This paper analyzes the behavior of stack-augmented recurrent neural network (RNN) models. Due to the architectural similarity between stack RNNs and pushdown transducers, we train stack RNN models on a number of tasks, including string reversal, context-free language modelling, and cumulative XOR evaluation. Examining the behavior of our networks, we show that stack-augmented RNNs can discover intuitive stack-based strategies for solving our tasks. However, stack RNNs are more difficult to train than classical architectures such as LSTMs. Rather than employ stack-based strategies, more complex networks often find approximate solutions by using the stack as unstructured memory.